The Gausian distribution, or Normal Distribution is an important and very widely used probability distribution. It is mainly defined by two parameters. The first is mean which is the average value of the feature vectors. The second parameter is the variance which measures how much the data is scattered around the mean.
If the mean of a normal distribution is zero and the variance is one then it is called standard normal distribution. Normal density is important for several cases. First of all, The `Central Limit Theorem`_ says that sum of independent identically distributed random variables approximate the normal distribution. So, considering the pattern recognition case, there will be very large set of feature vectors and classes, and independent of the probability distributions of features, the sum of the distributions is going to have a Normal Density.
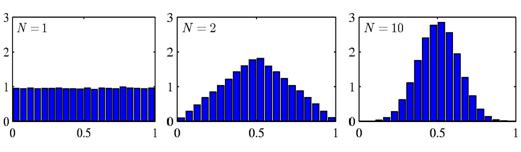
The following histograms of N uniformly distributed random variables for different values of N can be given to visualize the Central Limit Theorem.
On the other hand, there is a strong relation between the concept of entropy and Normal Distribution. The distribution that maximizes the differential entropy is Normal Distribution.
Probability Density Function(PDF) of Multivariate Gaussian is given by the equation:
[TODO: Insert the equation here!]
Where $ \Sigma $ is the covariance matrix and $ \mu $ is the mean vector (that is, the expected value) of a Normal Distribution is it's mean.