Fourier Optics is a sub-field of classical optics in which Fourier transforms are used as the main mathematical model of an optical system. In this article I will go over a simple example of how to use a Fourier transform to describe the diffraction pattern encountered when light passes through a slit aperture.
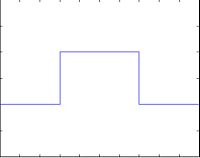
If we imagine that our slit aperture can be thought of as a spatial filter that only passes light through the slit and blocks light everywhere else, then it can be described mathematically as:
$ f(t)=\begin{cases} 1&\text{if } |t| < a\\ 0&\text{if } |t| > a\end{cases} $
where 2a is the width of the slit. Now, taking the Fourier transform of the aperture shape we get:
$ X(\omega)=\int_{ -a}^{a} {e }^{ -j\omega t} dx $
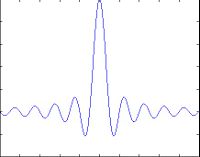
$ X(\omega)=2 \frac{ sin(\omega a)}{\omega} $
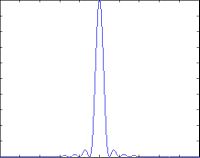
Which is a sinc function. What we have now is the diffraction pattern of the light, but what we really see when we look at light it its intensity. From physics classes you may remember that the intensity of light would now be given by the square modulus of the amplitude of the of light:
and this is a laser being passed through a slit aperture:
This method can also be used to show the famous diffraction pattern of Young's Double slit experiment, or if extended to two dimensions can show the diffraction pattern of light going through a rectangular aperture.
This is a good website with applets that let you play with rectangular, circular, and slit diffraction patterns: http://cnyack.homestead.com/files/afourtr/ftdiffraction.htm