You are living off campus and need to take the bus to get to class. The bus you need to get on is 5 minutes late 75% of the time, crowded 55% of the time, and full 10% of the time. If the bus is crowded, it takes an extra 3 minutes to get onto campus, and if the bus is full, the bus driver will not let you on the bus. It is also snowing 20% of the time which takes an extra 8 minutes to get to class. If there are no delays, it takes the bus 10 minutes to get you to campus and 6 minutes for you to walk to class. What is the probability of you making it to class on time if you have 24 minutes before the start of class?
Solution:
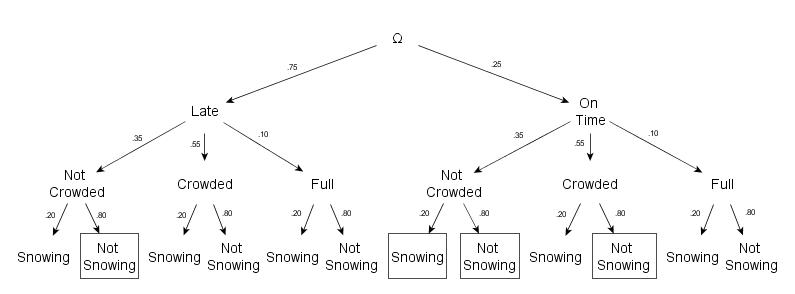
Without any delay, you are able to make it to class with 8 extra minutes to spare. After calculating the times the only situations in which you can make it on time are {(the bus is late, not crowded, not snowing), (the bus is on time, not crowded, snowing), (the bus is on time, not crowded, not snowing), (the bus is on time, crowded, not snowing)}. Therefore, the probability of you getting to class on time is:
[(.75)(.35)(.80)] + [(.25}(.35)(.20)] + [(.25)(.35)(.80)] + [(.25)(.55)(.80)]
= [.21] + [.0175] + [.07] + [.11]
= .4075
The probability of you getting to class on time is 40.75%.

