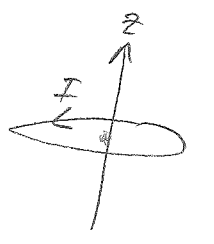
1)
a)
$ \frac{\partial}{\partial r}\bigg(r^2\frac{\partial\Phi}{\partial r}\bigg) + \frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\bigg(\sin\theta\frac{\partial \Phi}{\partial \theta}\bigg) =0 $
n =1 solution:
$ \begin{align*} \Phi (r,\theta) &= [Ar + \frac{B}{r^2}]\cos\theta\\ & = \begin{cases}Ar\cos\theta, r<a \hspace{3cm} \leftarrow\text{ no singularity at }r=0\\ -E_0r\cos\theta + \frac{B}{r^2}\cos\theta, r>a\hspace{1cm} \leftarrow\text{ aproach }E_0\hat{z} \text{ for } r\to\infty (E_0\hat{z} = -E_0r\cos\phi) \end{cases} \end{align*} $
\underline{BC's} : continuous at r = a:
$ Aa = -E_0a + \frac{B}{a^2} $
$ \rho_s = 0 \to D_{1n} = D_2n |_{r=a} \to \epsilon_0E_1 = \epsilon_0\epsilon_rE_2\to E_1 = \epsilon_rE_2 $
$ E = \frac{\partial\Phi}{\partial r}\hat{r} + \frac{1}{r}\frac{\partial\Phi}{\partial \theta}\hat{\theta} = \begin{cases}A\cos\theta\hat{r} - A\sin\theta\hat{\theta}\\ (-E_0\cos\theta - \frac{2B}{a^3}\cos\theta)\hat{r} + (E_0\sin\theta - \frac{B}{r^3}\sin\theta)\hat{\theta}\end{cases} $
at $ \theta = 0 $:
$ A = \epsilon_r\bigg[-E_0 - \frac{2B}{a^3}\bigg] = -E_0 + \frac{B}{a^3} $
$ -\epsilon_rE_0 - \frac{2\epsilon_r}{a^3}B = -E_0+\frac{B}{a^3} $
$ B\bigg[\frac{1+2\epsilon_r}{a^3}\bigg] = E_0(1-\epsilon_r) $
$ B = \frac{E_0(1-\epsilon_r)a^3}{1+2\epsilon_r} $
$ A = -E_0 + \frac{B}{a^3} $
$ = -E_0 + \frac{E_0(1-\epsilon_r)}{1+2\epsilon_r} $
$ = \frac{E_0(1-\epsilon_r) - E_0(1+2\epsilon_r)}{1+2\epsilon_r} = \frac{\cancel{E_0}-E_0\epsilon_r - \cancel{E_0}-2E_0\epsilon_r}{1+2\epsilon_r} $
$ A = \frac{-3E_0\epsilon_r}{1+2\epsilon_r} $
$ \theta=0 $: $ \bar{E} = \bigg[+E_0 - \frac{2B}{r^3}\bigg]\hat{z} $
$ \bar{J} = \sigma\bar{E} = +\sigma E_0 - \frac{2\sigma E_0a^3}{r^3}\bigg(\frac{1-\epsilon_r}{1+2\epsilon_r}\bigg) $
1)b)
If sphere is an insulator, $ \sigma 0 \to \bar{J} = \sigma\bar{E} = 0 $
2)a)
$ \nabla\times\bar{H} = \bar{J} + \frac{\partial D}{\partial t} = \sigma E + j\omega\epsilon E $
$ \oint\bar{H}\cdot d\bar{l} = \oint_S\bar{J}\cdot d\bar{s} + \frac{\partial}{\partial t}\oint_sD\cdot d\bar{s} $
$ \bar{A} = \int_v\frac{\mu_0\bar{J}e^{-jkR}}{4\pi R}dv $
$ \bar{A} = \frac{\mu_0I}{4\pi}\oint\frac{e^{-jkR}}{R}d\bar{l} $
$ \bar{A} = \frac{\mu_0I}{4\pi}\oint_0^{2\pi}e^{-jk\Gamma}d\phi $
$ \bar{A} = \frac{\mu_0I}{2}e^{-jk\Gamma}\hat{\phi} $
$ \nabla\times\bar{E} =-\frac{\partial \bar{B}}{\partial t} $
$ \oint\bar{E}\cdot d\bar{l} = \frac{\partial}{\partial t}\oint_s\bar{B}\cdot d\bar{s} $
$ \bar{H} = \frac{1}{\mu}\nabla\times\bar{A}\text{ (single loop)} $
$ k = \omega\sqrt{\mu_0\epsilon_c} = \omega\sqrt{\mu_0\bigg(1+\frac{\sigma}{\sqrt{\omega}}\bigg)\epsilon_0} $
$ R = \Gamma $
$ \bar{J}dv = JSdl = Idl $
$ dl = \Gamma d\phi $
$ \bar{B} = \nabla\times\bar{A} = \frac{1}{p}\begin{vmatrix}\hat{p}&p\hat{\phi}&\hat{z}\\\frac{\partial}{\partial p}&\frac{\partial}{\partial \phi}&\frac{\partial}{\partial z}\\0&pA_\phi&0\end{vmatrix} = \hat{z}\bigg[\frac{1}{p}\frac{\partial}{\partial p}pA_\phi\bigg] = \hat{z}\bigg[\frac{1}{p}\frac{\partial}{\partial p}\frac{\mu_0I}{2}pe^{-jkp}\bigg] $
$ \bar{B} = \hat{z}\bigg[\frac{1}{p}\bigg]\bigg(\frac{\mu_0I}{2}\bigg)(-jkpe^{-jkp} + e^{-jkp}) =\hat{z}\bigg(\frac{\mu_0I}{2}\bigg)(-jke^{-jkp} + \frac{1}{p}e^{-jkp}) $
$ \bar{H} = \hat{z}\bigg(\frac{I}{2}\bigg)(-jke^{-jkp} + \frac{1}{p}e^{-jkp}) $
b)
$ P = \frac{1}{2}\int\sigma E^2dv $
c)
$ z = \frac{V_0}{I_0} = \frac{\int E\cdot d\bar{l}}{\int\bar{J}\cdot d\bar{s}} $