2)
$ \Gamma= \frac{Z_{in} - Z_o}{Z_{in} + Z_{o}} $
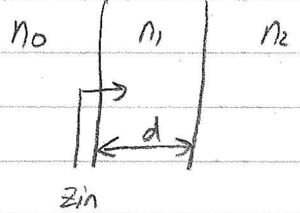
$ Z_{in} = Z_1\bigg(\frac{Z_2 + j Z_1\tan(\beta l)}{Z_1 + jZ_2 \tan(\beta l)}\bigg) $
$ Z_{in} = n_1\bigg(\frac{n_2 + j n_1\tan(\beta_1 d)}{n_1 + jn_2 \tan(\beta_1 d)}\bigg) $
$ \left\{ \begin{array}{ll} n_i = \sqrt{\frac{\mu_o}{\epsilon_i}} = \sqrt{\frac{\mu_o}{\epsilon_o}}\frac{1}{\sqrt{\epsilon_r}} = \frac{n_o}{n_i}\\ \beta_i = \omega\sqrt{\mu_o\epsilon_o}\sqrt{\epsilon_r} = \beta_on_i \end{array} \right. $
$ \Gamma = \frac{n_1(n_2 + j n_1\tan(\beta_1 d)) - n_0(n_1 + j n_2\tan(\beta_1 d))}{n_1(n_2 + j n_1\tan(\beta_1 d)) + n_0(n_1 + j n_2\tan(\beta_1 d))} $
$ \Gamma = \frac{n_1n_2 - n_0n_1 + (n_1^2 - n_0n_2)( j\tan(\beta_1 d))}{n_1n_2 + n_0n_1 + (n_1^2 + n_0n_2)( j\tan(\beta_1 d))} $
$ \left\{ \begin{array}{ll} n_1n_2 = n_0^2(1/n_1n_2)\hspace{0.5cm}\beta_1d = \beta_0n_1d\\ n_0n_1 = n_0^2(1/n_0n_1)\\ n_1^2 = n_0^2(1/n_1^2)\\ n_0n_2 = n_0^2(1/n_0n_2)\\ \end{array} \right. $
$ \Gamma = \frac{(1/n_1n_2) - (1/n_0n_1) + (1/n_1n_1 - 1/n_0n_2)(j\tan(\beta_0n_1d))}{(1/n_1n_2) + (1/n_0n_1) + (1/n_1n_1 + 1/n_0n_2)(j\tan(\beta_0n_1d))} $
$ \Gamma = \frac{n_0n_1 - n_1n_2 + (n_0n_2 - n_1^2)(j\tan(\beta_0n_1d))}{n_0n_1 + n_1n_2 + (n_0n_2 + n_1^2)(j\tan(\beta_0n_1d))} $
$ \bar{E}_r = \hat{x}(\Gamma)e^{j\beta Z}\hspace{0.5cm}\beta_o = \omega\sqrt{\mu_o\epsilon_o} $
3)
$ T = \frac{2n_2}{n_2+n_1} = \frac{\frac{2}{n_2}}{\frac{1}{n_2} + \frac{1}{n_1}} = \frac{2n_1}{n_2+n_1} $
$ T = \frac{n_2-n_1}{n_2+n_1} = \frac{\frac{1}{n_2} - \frac{1}{n_1}}{\frac{1}{n_2} + \frac{1}{n_1}} = \frac{n_1-n_2}{n_2+n_1} $
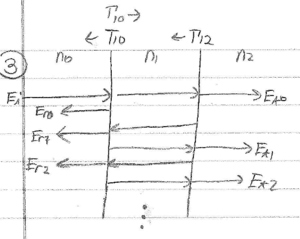
$ \begin{align*} \bar{E}_o = \hat{x}E_i[e^{-j\beta Z} &+ \Gamma_ae^{j\beta Z} + (1+\Gamma_a)(\Gamma_{12}T_{10})e^{e^{j\beta Z}}\\ &+ (1+\Gamma_a)(\Gamma_{12}\Gamma_{10})(\Gamma_{12}T_{10})e^{j\beta Z}\\ &+ (1+\Gamma_a)(\Gamma_{12}\Gamma_{10})^2(\Gamma_{12}T_{10})e^{j\beta Z} \text{ Let <math>E_i = 1<math>} \end{align*} $
$ E_r = \Gamma_a + (1+\Gamma_a)\sum_{n=0}^N(\Gamma_{12}\Gamma_{10})^n(\Gamma_{12}T_{10}) $
$ E_r = \Gamma_a + (1+\Gamma_a)\sum_{n=0}^N\big(\frac{n_1-n_2}{n_1+n_2}\big)^n\big(\frac{n_1-n_0}{n_1+n_0}\big)^n\big(\frac{n_1-n_2}{n_1+n_2}\big)\big(\frac{2n_0}{n_0+n_1}\big) $
where $ \Gamma_a=\Gamma $ from part a)
4)
a) $ n_2 = n_0 $ and
$ \begin{align*} \beta_1d &= n(\pi) \text{ where: n=0,1,2,3, \dots}\\ \bigg(\frac{2\pi}{\lambda_1}\bigg)d &= n(\pi)\\ d&=\frac{n\lambda_1}{2} \end{align*} $
b) $ n_2 = \frac{n_1^2}{n_0} $ and
$ \begin{align*} \beta_1d &= \frac{\pi}{2} + n\pi = \frac{\pi}{2}(1+2n) \text{ n=0,1,2,3,\dots}\\ \bigg(\frac{2\pi}{\lambda_1}\bigg)d &= \frac{\pi}{2}(1+2n)\\ d&= \frac{\lambda_1}{4}(1+2n) \text{ n=0,1,2,3, \dots} \end{align*} $
Note: $ \lambda_1 = \frac{2\pi}{\beta_1} = \frac{c}{fn_1} $
5) from a) in 4:
$ n_1 = \sqrt{n_0n_2} \hspace{0.8cm} d= \bigg(\frac{\lambda_1}{4}\bigg)(2n+1) = \bigg(\frac{2\pi c}{4\omega n_1}\bigg)(2n+1) = \bigg(\frac{\pi c}{2\omega n_1}\bigg)(2n+1) $
Requirements:
a) distance must be an odd multiple of $ \lambda/4 $, where $ \lambda $ is the wavelength of the incident wave.
b) the refractive index must be: $ \sqrt{n_0n_2} $