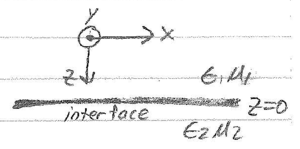
$ \left\{ \begin{array}{ll} \bar{E}_1 = \hat{x}E_{io}e^{-j\beta_1Z} + \hat{x}(rE_{io})e^{+j\beta_1Z}\\ \bar{H}_1 = \hat{y}\frac{E_{io}}{n_1}e^{-j\beta_1Z} - \hat{y}\big(\frac{rE_{io}}{n_1}\big)e^{+j\beta_1Z}\\ \bar{E}_2 = \hat{x}(tE_{io})e^{-j\beta_2Z}\\ \bar{H}_2 = \hat{y}\frac{tE_{io}}{n_2}e^{-j\beta_2Z} \end{array} \right. $
$ \left\{ \begin{array}{ll} \beta_i = \omega\sqrt{\mu_i\epsilon_i}<br> n_i= \sqrt{\frac{\mu_i}{\epsilon_i}}<br> \end{array} \right. $
BC's (at $ z = 0 $) :
$ \label{eq1}E_{1t} = E_{2t} $ (1)
$ D_{1n} = D_{2n} = 0 $ (2)
$ \label{eq3}H_{1t} = H_{2t} $ (3)
$ B_{1n} = B_{2n} =0 $ (4)
(1) $ \to E_{io} + r E_{io} = t E_{io} $
$ 1+r=t $
(3) $ \to \frac{E_{io}}{n_1} -\frac{rE_{io}}{n_1} = \frac{tE_{io}}{n_2} $
$ \hspace{0.8cm}\frac{n_2}{n_1}(1-r) = t $
2 equations, 2 unknowns: $ r, t $
$ \frac{n_2}{n_1}(1-r) =1+r $
$ r\big(1+\frac{n_2}{n_1}\big) = \frac{n_2}{n_1} -1 $
$ r=\frac{ \frac{n_2}{n_1} -1}{\frac{n_2}{n_1}+1} $
$ r = \frac{n_2-n_1}{n_2+n_1} $
$ t=1+r $
$ t = 1+\frac{n_2-n_1}{n_2+n_1} $
$ t = \frac{2n_2}{n_2+n_1} $