1)
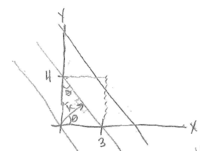
$ \begin{align*} \bar{k} &= k_x\hat{x} + k_y\hat{y}\\ &=\frac{2\pi}{\lambda x}\hat{x} + \frac{2\pi}{\lambda y}\hat{y}\\ &=\frac{2\pi}{3}\hat{x} +\frac{2\pi}{4}\hat{y}\\ |\bar{k}| &= \sqrt{\frac{4\pi^2}{9} + \frac{4\pi^2}{16}} = \beta=\frac{\omega}{c}\\ \omega &= c\frac{\frac{4\pi^2(25)}{144}} = \frac{10\pi c}{12} = \frac{10\pi}{4}\cdot10^8\\ f &= \frac{\omega}{2\pi} = \frac{5}{4}\cdot10^8\frac{1}{5} \end{align*} $
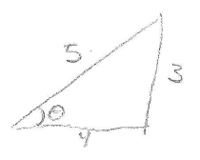
$ \left\{ \begin{array}{ll} \bar{k} = k(\hat{x}\cos\theta+\hat{y}\sin\theta)\\ \cos\theta = \frac{\lambda}{3}\\ \sin\theta = \frac{\lambda}{4}\\ \end{array} \right.\\ \bar{k} = \frac{2\pi}{\lambda}\big(\hat{x}\frac{\lambda}{3}+\hat{y}\frac{\lambda}{4}\big) = \big(\hat{x}\frac{2\pi}{3}+\hat{y}\frac{2\pi}{4}\big) $
2)
$ \begin{align*} \bar{k} &= \beta\cos\theta\hat{x} + \beta\sin\theta\hat{y}\\ \beta_0\cos\theta &= \frac{2\pi}{3}\\ \cos\theta =\frac{2\pi}{3}\bigg[\frac{1}{|k|}\bigg] &= \frac{2\pi}{3}\bigg[\frac{12}{10\pi}\bigg] = \frac{4}{5} \\ \theta &= \cos^{-1}\big( \frac{4}{5}\big)=35^\circ \end{align*} $
$ \beta_0\sin\theta=\frac{2\pi}{4} \sin\theta = \big(\frac{\pi}{2}\big)\big(\frac{12}{10\pi}\big) \sin\theta = \frac{3}{5} $
3)
$ k=\frac{2\pi}{3}\hat{x} + \frac{2\pi}{4}\hat{y} |k| = \frac{5\pi}{6} \lambda_x = 3m \lambda_y = 4m $
4)
$ \bar{E} = E_0e^{-j(\bar{k}\cdot\bar{r})} = E_0e^{-j\big(\frac{2\pi}{3}x +\frac{\pi}{2}y\big)} \bar{E}(x=0) = E_0e^{-j\big(\frac{\pi}{2}y\big)} $
$ \tan\big(\frac{2\pi}{\lambda}\frac{\lambda}{2}\big)=\tan\pi=0\\ Z_{in} = \frac{Z_0(Z_i)}{Z_0} = Z_i\\ \underline{\textbf{at top antenna}}: \bar{E} - E_0e^{-j(\frac{\pi}{2})(y_0+1)}\\ \underline{\textbf{at bottom antenna}}: \bar{E} - E_0e^{-j(\frac{\pi}{2})y_0}\\ then: \frac{|v_1+v_2|}{|v_1|} = \frac{|E_0e^{-j(\frac{\pi}{2})y_0}[1+e^{-j\frac{\pi}{2})}]|}{|E_0e^{-j(\frac{\pi}{2})y_0}|}=|1+\cos(\frac{\pi}{2}) -j\sin\frac{\pi}{2}|=|1+0-j|\\ = \sqrt{2} $
5)
$ \bar{E}|_{x=0} = E_0e^{-j(0+0)} = E_0 \frac{|v_1+v_2|}{|v_1|} = \frac{|E_0+E_0|}{|E_0|} = \frac{2|E_0|}{|E_0|} =2 $
6)
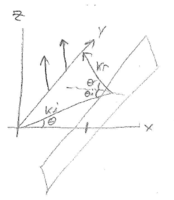
$ \begin{align*} \bar{E}_i &= E_0e^{-j(\frac{2\pi}{3}x+\frac{2\pi}{4}y)}\hat{k}_i\\ \bar{E}_r &= \Gamma E_0e^{-j(-\frac{2\pi}{3}x+\frac{2\pi}{4}y)}\hat{k}_r \end{align*} $
---only $ x $ component changes
---for maximum $ v $ want maximum $ |\bar{E}| $
---$ \Gamma = -1 $
$ \bar{E} = \bar{E}_i + \bar{E}_r = E_0[e^{-j(\frac{2\pi}{3}x+\frac{2\pi}{4}y)}\hat{k}_i - e^{-j(-\frac{2\pi}{3}x+\frac{2\pi}{4}y)}\hat{k}_r] \bar{k}_i = \cos\theta_i\hat{x} + \sin\theta_i\hat{y} k_r = -\cos\theta_i\hat{x} + \sin\theta_i\hat{y} $
$ \to \text{maximum of }\cos\theta \text{ is }1 \text{ so, } x = 3m: $
$ \bar{E}_r = E_0[-e^{j(2\pi)}e^{-j(\frac{\pi}{2})y}\hat{k}_r] = -E_0e^{-j(\frac{\pi}{2})y}\hat{k}_r $
7)
$ V_{out}=V_1+V_2=0=E_1+E_2 E_0e^{-j(\frac{\pi}{2})y_0} + E_0e^{-j(\frac{\pi}{2})y_0+1} =0 E_0e^{-j(\frac{\pi}{2})y_0}[1 + e^{-j(\frac{\pi}{2}+\phi)}] =0 $
must add phase of $ \phi = \frac{\pi}{2} $
$ 1+e^{-j(\pi)} = 1+(-1) = 0 $
length of $ T_1: \frac{\lambda}{2} = \frac{\pi}{\beta} = T_1 $
length of $ T_2: \lambda = \frac{2\pi}{\beta} = T_2 $
$ T_2-T_1 = \frac{\pi}{\beta} = \frac{\lambda}{2} $