Communication, Networking, Signal and Image Processing (CS)
Question 3: Communications
August 2011
Contents
[hide]Question
Problem 1. Suppose a system is monitored daily, except on Sundays, because it is faulty half of the time. On Mondays, Wednesdays, and Fridays at noon, if everything checks out fine, a sensor sends a signal with amplitude $ -A $, where $ A $ is a positive constant, millivolts along a pair of wires. However, if there is a fault, the sensor sends a signal with amplitude $ A $ millibolts along the pair of wires. In both cases the duration of the signal from the sensor is ten seconds. The signals are fliped on Tuesdays, Thursdays, and Saturdays, that is, the positive polarity indicates that everything is fine and negative polarity indicates that there is a fault on these days. The additive white Gaussian two-sided noise power spectral density on the wires is $ N_0 $/2 = 5x$ 10^{-6} $ $ V^2 $/$ Hz $.
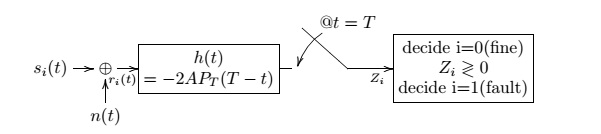
(a) Precisely define a receiver structure that takes the signal from the pairs of wires in order to determine whether a fault exists in the system from the pair of wires in order to determine whether a fault exists in the system on Mondays, Wednesdays, and Fridays. The receiver must minimize the probability of being wrong in this fault assessment. If there is any filtering of the signal on the wire, sampling, or comparison with a threshold in your design, precisely define all filters, sampling times, and threshold values.
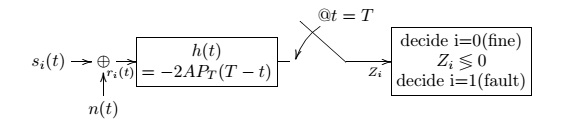
(b) Explain how the system that you designed in Part (a) should be modified to work on Tuesdays, Thursdays, and Saturdays.
(c) Find the probability that the optimal system-fault-detecting receiver (of Part (a)) is wrong in its assessment of the condition of the system.
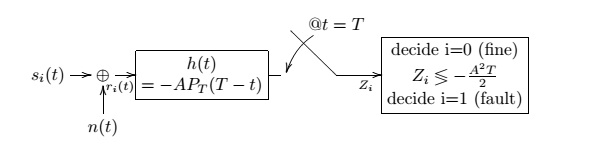
(d) Suddenly, the system is fixed and works perfectly, but now the clocked power to the sensor begins to fail so that half of the weeks the sensor works perfectly as described and half of the weeks it sends no signal at all. Precisely define (as before) a receiver structure that begins working at noon on Monday to detect whether the sensor is working or not and that minimizes the probability of being wrong in this assessment. It must report its answer by Sunday.
(e) Find the probability that the optimal sensor-fault-detecting receiver (of Part (d)) is wrong in its assessment of the condition of the sensor.
(f) How does your receiver design change in Part (d) if, because of temperature changes in the system, the two-sided noise power spectral density becomes 10x$ 10^{-6} $ $ V^2 $/$ Hz $ on Tuesdays, Thursdays, and Saturdays and remains at 5x$ 10^{-6} $ $ V^2 $/$ Hz $ on Mondays, Wednesdays, and Fridays?
Solution 1
$ \color{black}\text{(a) } T=10sec $
$ \color{black} s_0(t)=-A P_T(t), s_1(t)=A P_T(t) $
$ \color{black} h(t)=s_0(T-t)-s_1(T-t)=-2A P_T(T-t) $
$ \color{black} \mu_0=s_0(t)*h(t)|_{t=T}=2A^2T $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=-2A^2T $
$ \color{black} r_m=\frac12(\mu_0+\mu_1)=0 $
$ \color{black}\text{(b) } T=10sec $
$ \color{black} s_0(t)=A P_T(t), s_1(t)=-A P_T(t) $
$ \color{black} h(t)=-2A P_T(T-t) $
$ \color{black} \mu_0=s_0(t)*h(t)|_{t=T}=-2A^2T $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=2A^2T $
$ \color{black} r_m=\frac12(\mu_0+\mu_1)=0 $
$ \color{black}\text{(c) } \mu_1=-2A^2T=-20A^2 $
$ \color{black} \sigma^2=\frac{N_0}{2}\parallel h\parallel^2=\frac{N_0}{2}\cdot4A^2T=5\times10^{-6}\cdot4A^2\cdot10=2\times10^{-4}\cdot A^2 $
$ \color{black} P_{e,avg}=Q(\frac{r_m-\mu_1}{\sigma})=Q(\frac{0-(-20A^2)}{\sqrt{2\times10^{-4}\cdot A^2}})=Q(\frac{20A^2}{\sqrt{2}\times10^{-2}\cdot A})=Q(1000\sqrt{2}A) $
$ \color{black}\text{(d) } \text{Mondays, Wednesdays, and Fridays} $
$ \color{black} s_0(t)=-AP_T(t), s_1(t)=0 $
$ \color{black} h(t)=s_0(T-t)-s_1(T-t)=-AP_T(T-t) $
$ \color{black} \mu_0=s_0(t)*h(t)|_{t=T}=A^2T $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=0 $
$ \color{black} r_m=\frac{1}{2}(\mu_0+\mu_1)=\frac{1}{2}(A^2T+0)=\frac{A^2T}{2} $
$ \color{black} \text{Tuesdays, Thursdays, and Saturdays} $
$ \color{black} s_0(t)=AP_T(t), s_1(t)=0 $
$ \color{black} h(t)=-AP_T(T-t) $
$ \color{black} \mu_0=s_0(t)*h(t)|_{t=T}=-A^2T $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=0 $
$ \color{black} r_m=\frac{1}{2}(\mu_0+\mu_1)=\frac{1}{2}(-A^2T+0)=-\frac{A^2T}{2} $
$ \color{black} \text{Sundays } $
$ \color{black} \text{We cannot detect whether the sensor is working or not on Sunday.} $
$ \color{black}\text{(e) } \sigma^2=\frac{N_0}{2}\parallel h\parallel^2=\frac{N_0}{2}\cdot A^2T=5\times10^{-6}\cdot A^2\cdot10=5\times10^{-5}\cdot A^2 $
$ \color{black} \text{Mondays, Wednesdays, and Fridays} $
$ \color{black} P_{e,avg}=Q(\frac{\mu_0-\mu_1}{2\sigma})=Q(\frac{A^2T-0}{2\sigma})=Q(\frac{A^2\cdot10}{2\sqrt{5\times10^{-5}\cdot A^2}})=Q(500\sqrt{2}A) $
$ \color{black} \text{Tuesdays, Thursdays, and Saturdays} $
$ \color{black} P_{e,avg}=Q(\frac{\mu_0-\mu_1}{2\sigma})=Q(\frac{0-(-A^2T)}{2\sigma})=Q(500\sqrt{2}A) $
$ \color{black} \therefore P_{e,avg}=Q(500\sqrt{2}A) $
$ \color{black} \text{(f) The receiver does not need to change. The change of noise power spectral density affects only the error probability.} $
Solution 2
$ \color{red} \text{We can define } h(t)=c(s_0(T-t)-s_1(T-t))\text{ where c=constant.} $
$ \color{red} \text{Thus, the signs and values of } Z_i \text{ can change depending on } c\text{ and the threshold device can also change.} $
$ \color{red} \text{However, the signs and values of } Z_i \text{ does not affect on the probability that the receiver is wrong.} $
$ \color{black} s_i(t)=(-1)^iAP_T(t) (\text{where } T=10s) $
$ \color{black} n(t)\rightarrow S_n(f)=\frac{N_0}{2}=5\text{x}10^{-6} V^2/Hz $
$ \color{black} \text{(a) Define a receiver structure (Mondays, Wednesdays, and Fridays)} $
$ \color{black} Z_i=r(t)*h(t)|_{t=T}=s_i(t)*h(t)|_{t=T}+n(t)*h(t)|_{t=T}=\tilde{s}_i(T)+\tilde{n}(T) $
$ \color{red} \text{The difference between this and solution 1-(a) is because of the difference of constant } c \text{ in } h(t)=c(s_0(T-t)-s_1(T-t)). $
$ \color{black} \text{(b) Define a receiver structure (Tuesdays, Thursdays, and Saturdays)} $
$ \color{red} \text{The difference between this and solution 1-(b) is because of the difference of constant } c \text{ in } h(t)=c(s_0(T-t)-s_1(T-t)). $
$ \color{black} \text{(c) } s_1(t)=-AP_T(t) $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=-AT $
$ \color{black} \sigma^2=\frac{N_0}{2}\parallel h \parallel^2=\frac{N_0}{2}T $
$ \color{black} P_{e,avg}=P_{e,m}=Q(\frac{0-(-AT)}{\sigma})=Q(A\sqrt{\frac{2T}{N_0}}) $
$ \color{red} \text{This is the same as solution 1-(c). } $
$ \color{black}\text{(d) Define a receiver structure} $
$ \color{black} \text{- Mondays, Wednesdays, and Fridays} $
$ \color{black} s_0(t)=-AP_T(t), s_1(t)=0 $
$ \color{black} \mu_0=s_0(t)*h(t)|_{t=T}=-AT $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=0 $
$ \color{black} \text{threshold value } r_m=\frac{1}{2}(\mu_0+\mu_1)=-\frac{AT}{2} $
$ \color{black} \text{- Tuesdays, Thursdays, and Saturdays} $
$ \color{black} s_0(t)=AP_T(t), s_1(t)=0 $
$ \color{black} \mu_0=s_0(t)*h(t)|_{t=T}=AT $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=0 $
$ \color{black} \text{threshold value } r_m=\frac{1}{2}(\mu_0+\mu_1)=\frac{AT}{2} $
$ \color{black} \text{- Sundays } $
$ \color{black} \text{It is impossible to detect whether the sensor is working or not.} $
$ \color{red} \text{The difference between this and solution 1-(d) is because of the difference of constant } c \text{ in } h(t)=c(s_0(T-t)-s_1(T-t)). $
$ \color{black}\text{(e) } s_1(t)=s_{1,(M,W,F)}(t)=s_{1,(T,Th,S)}(t)=0 $
$ \color{black} \mu_1=s_1(t)*h(t)|_{t=T}=0 $
$ \color{black} \sigma^2=\frac{N_0}{2}\parallel h\parallel^2=\frac{N_0}{2}\cdot T $
$ \color{black} P_{e,m,(M,W,F)}=Q(\frac{0-(-\frac{AT}{2})}{\sigma})=Q(\frac{A}{2}\sqrt{\frac{2T}{N_0}}) $
$ \color{black} P_{e,m,(T,Th,S)}=Q(\frac{\frac{AT}{2}-0}{\sigma})=Q(\frac{A}{2}\sqrt{\frac{2T}{N_0}}) $
$ \color{black} \therefore P_{e,avg}=P_{e,m,(M,W,F)}=P_{e,m,(T,Th,S)}=Q(\frac{A}{2}\sqrt{\frac{2T}{N_0}}) $
$ \color{red} \text{This is the same as solution 1-(e). } $
$ \color{black} \text{(f) The receiver is same as that of Part (d).} $
Related Problem
Suppose a system is monitored daily, because it is faulty half of the time. A sensor sends different signals every 3 days. On the first day, if everything checks out fine, the sensor sends a signal with amplitude $ A $, where $ A $ is a positive constant, millivolts along a pair of wires. However, if there is a fault, the sensor sends a signal with amplitude $ -A $ millibolts along the pair of wires. In both cases the duration of the signal from the sensor is one seconds. On the second day, the signals change $ -2A $ for fine, $ 2A $ for fault. On the third day, the signals change $ -3A $ for fine, $ 3A $ for fault. The additive white Gaussian two-sided noise power spectral density on the wires is $ N_0 $/2 = 10x$ 10^{-6} $ $ V^2 $/$ Hz $.
(a) Precisely define a receiver structure that takes the signal from the pairs of wires in order to determine whether a fault exists in the system from the pair of wires in order to determine whether a fault exists in the system on the first day. The receiver must minimize the probability of being wrong in this fault assessment. If there is any filtering of the signal on the wire, sampling, or comparison with a threshold in your design, precisely define all filters, sampling times, and threshold values.
(b) Explain how the system that you designed in Part (a) should be modified to work on the second day.
(c) If you use the same threshold device as that of Part (a), explain how the filter you designed in Part (a) should be modified to work on the third day.
(d) Find the probability that the optimal system-fault-detecting receiver (of Part (c)) is wrong in its assessment of the condition of the system.