3.2 Systems with Stochastic Inputs
Given a random process $ \mathbf{X}\left(t\right) $ , if we assign a new sample function $ \mathbf{Y}\left(t,\omega\right) $ to each sample function $ \mathbf{X}\left(t,\omega\right) $ , then we have a new random process $ \mathbf{Y}\left(t\right) $ : $ \mathbf{Y}\left(t\right)=T\left[\mathbf{X}\left(t\right)\right] $ .
Note
We will assume that $ T $ is deterministic (NOT random). Think of $ \mathbf{X}\left(t\right)=\text{input to a system} $. $ \mathbf{Y}\left(t\right)=\text{output of a system} $.
$ \mathbf{Y}\left(t,\omega\right)=T\left[\mathbf{X}\left(t,\omega\right)\right],\quad\forall\omega\in\mathcal{S} $.
In ECE, we are often interested in finding a statistical description of $ \mathbf{Y}\left(t\right) $ in terms of that of $ \mathbf{X}\left(t\right) $ . For general $ T\left[\cdot\right] $ , this is very difficult. We will look at two special cases:
1. Memoryless system
2. Linear time-invariant system
3.2.1 Memoryless System
Definition
A system is called memoryless if its output $ \mathbf{Y}\left(t\right)=g\left(\mathbf{X}\left(t\right)\right) $ , where $ g:\mathbf{R}\rightarrow\mathbf{R} $ is only a function of its current argument $ x $ .
• $ g\left(\cdot\right) $ is not a function of the past or future values of input.
• $ \mathbf{Y}\left(t\right)=g\left(\mathbf{X}\left(t\right)\right) $ depends only on the instantaneous value of $ \mathbf{X}\left(t\right) $ at time $ t $ .
Example
Square is a memoryless system.
$ g\left(x\right)=x^{2}. $
$ \mathbf{Y}\left(t\right)=g\left(\mathbf{X}\left(t\right)\right)=\mathbf{X}^{2}\left(t\right). $
Example
Integrators are NOT memoryless. They have memory of the past.
$ \mathbf{Y}\left(t\right)=\int_{-\infty}^{t}\mathbf{X}\left(\alpha\right)d\alpha. $
$ \mathbf{Y}\left(t,\omega\right)=\int_{-\infty}^{t}\mathbf{X}\left(\alpha,\omega\right)d\alpha. $
Note
For memoryless systems, the first-order density $ f_{\mathbf{Y}\left(t\right)}\left(y\right) $ of $ \mathbf{Y}\left(t\right) $ can be expressed in terms of the first-order density of $ \mathbf{X}\left(t\right) $ and $ g\left(\cdot\right) $ . This is just a simple function of a random variable. Also $ E\left[\mathbf{Y}\left(t\right)\right]=E\left[g\left(\mathbf{X}\left(t\right)\right)\right]=\int_{-\infty}^{\infty}g\left(x\right)f_{\mathbf{X}\left(t\right)}\left(x\right)dx $ and $ R_{\mathbf{YY}}\left(t_{1},t_{2}\right)=E\left[\mathbf{Y}\left(t_{1}\right)\mathbf{Y}\left(t_{2}\right)\right]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g\left(x_{1}\right)g\left(x_{2}\right)f_{\mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)}\left(x_{1},x_{2}\right)dx_{1}dx_{2}. $
Also, you can get the n-th order pdf of $ \mathbf{Y}\left(t\right) $ using the mapping $ \mathbf{Y}\left(t_{1}\right)=g\left(\mathbf{X}\left(t_{1}\right)\right),\cdots,\mathbf{Y}\left(t_{n}\right)=g\left(\mathbf{X}\left(t_{n}\right)\right) $ .
Theorem
Let $ \mathbf{X}\left(t\right) $ be a S.S.S. random process that is the input to a memoryless system. Then the output \mathbf{Y}\left(t\right) is also a S.S.S. random process.
Example. Hard limiter
Consider a memoryless system with
$ g\left(x\right)=\left\{ \begin{array}{lll} +1 ,x>0\\ -1 ,x\leq0. \end{array}\right. $
Consider $ \mathbf{Y}\left(t\right)=g\left(\mathbf{X}\left(t\right)\right)=\textrm{sgn}\left(\mathbf{X}\left(t\right)\right) $ . Find $ E\left[\mathbf{Y}\left(t\right)\right] $ and $ R_{\mathbf{YY}}\left(t_{1},t_{2}\right) $ given the “statistics” of $ \mathbf{X}\left(t\right) $ .
Solution
$ E\left[\mathbf{Y}\left(t\right)\right]=\left(+1\right)\cdot P\left(\left\{ \mathbf{Y}\left(t\right)=+1\right\} \right)+\left(-1\right)\cdot P\left(\left\{ \mathbf{Y}\left(t\right)=-1\right\} \right) $$ =\left(+1\right)\cdot\left(1-F_{\mathbf{X}\left(t\right)}\left(0\right)\right)+\left(-1\right)\cdot F_{\mathbf{X}\left(t\right)}\left(0\right)=1-2F_{\mathbf{X}\left(t\right)}\left(0\right). $
$ R_{\mathbf{YY}}\left(t_{1},t_{2}\right)=E\left[\mathbf{Y}\left(t_{1}\right)\mathbf{Y}\left(t_{2}\right)\right]=\left(+1\right)\cdot P\left(\left\{ \mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)>0\right\} \right)+\left(-1\right)\cdot P\left(\left\{ \mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)\leq0\right\} \right) $
where $ P\left(\left\{ \mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)>0\right\} \right)=\int_{0}^{\infty}\int_{0}^{\infty}f_{\mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)}\left(x_{1},x_{2}\right)dx_{1}dx_{2}+\int_{-\infty}^{0}\int_{-\infty}^{0}f_{\mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)}\left(x_{1},x_{2}\right)dx_{1}dx_{2} $ .
Example
$ \mathbf{X}\left(t\right)=\mathbf{A}\cdot\cos\left(\omega_{0}t+\mathbf{\Theta}\right) $ where $ \mathbf{A} $ and $ \mathbf{\Theta} $ are independent random variables and $ \mathbf{\Theta}\sim u\left[0,2\pi\right) $ . Assume that $ \mathbf{A} $ has a mean $ \mu_{\mathbf{A}} $ and a variance $ \sigma_{\mathbf{A}}^{2} $ . Is $ \mathbf{X}\left(t\right) $ a WSS random process?
Solution
• Check whether $ E\left[\mathbf{X}\left(t\right)\right] $ is constant or not: $ E\left[\mathbf{X}\left(t\right)\right] $
• Check whether $ R_{\mathbf{XX}}\left(t_{1},t_{2}\right)=R_{\mathbf{X}}\left(\tau\right) : $ $ R_{\mathbf{XX}}\left(t_{1},t_{2}\right) = E\left[\mathbf{X}\left(t_{1}\right)\mathbf{X}\left(t_{2}\right)\right] $$ =E\left[\mathbf{A}\cdot\cos\left(\omega_{0}t_{1}+\mathbf{\Theta}\right)\cdot\mathbf{A}\cdot\cos\left(\omega_{0}t_{2}+\mathbf{\Theta}\right)\right] $$ =E\left[\mathbf{A}^{2}\right]\cdot E\left[\cos\left(\omega_{0}t_{1}+\mathbf{\Theta}\right)\cdot\cos\left(\omega_{0}t_{2}+\mathbf{\Theta}\right)\right] $$ =\left(\sigma_{\mathbf{A}}^{2}+\mu_{\mathbf{A}}^{2}\right)\cdot E\left[\cos\left(\omega_{0}t_{1}+\mathbf{\Theta}\right)\cdot\cos\left(\omega_{0}t_{2}+\mathbf{\Theta}\right)\right] $$ =\left(\sigma_{\mathbf{A}}^{2}+\mu_{\mathbf{A}}^{2}\right)\cdot\left\{ \frac{1}{2}E\left[\cos\left(\omega_{0}\left(t_{1}+t_{2}\right)+\mathbf{2\Theta}\right)\right]+\frac{1}{2}E\left[\cos\left(\omega_{0}\left(t_{1}-t_{2}\right)\right)\right]\right\} $$ =\frac{1}{2}\left(\sigma_{\mathbf{A}}^{2}+\mu_{\mathbf{A}}^{2}\right)\cos\left(\omega_{0}\left(t_{1}-t_{2}\right)\right). $
• $ \therefore\mathbf{X}\left(t\right) $ is WSS.
Recall
$ \cos\alpha\cos\beta=\frac{1}{2}\left\{ \cos\left(\alpha+\beta\right)+\cos\left(\alpha-\beta\right)\right\} $ .
3.2.2 LTI (Linear Time-Invariant) system
Linear Systems
A linear system L\left[\cdot\right] is a transformation rule satisfying the following properties.
1. $ L\left[\mathbf{X}_{1}\left(t\right)+\mathbf{X}_{2}\left(t\right)\right]=L\left[\mathbf{X}_{1}\left(t\right)\right]+L\left[\mathbf{X}_{2}\left(t\right)\right] $ .
2. $ L\left[\mathbf{A}\cdot\mathbf{X}\left(t\right)\right]=\mathbf{A}\cdot L\left[\mathbf{X}\left(t\right)\right] $ .
Time-invariant
A (linear) system is time-invariant if, given response $ \mathbf{Y}\left(t\right) $ for an input $ \mathbf{X}\left(t\right) $ , it has response $ \mathbf{Y}\left(t+c\right) $ for input $ \mathbf{X}\left(t+c\right) $ , for all $ c\in\mathbb{R} $ .
LTI
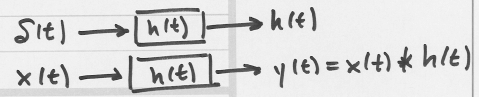
A linear time-invariant system is one that is both linear and time-invariant. A LTI system is characterized by its impulse response $ h\left(t\right) $ :
If we put a random process $ \mathbf{X}\left(t\right) $ into a LTI system, we get a random process $ \mathbf{Y}\left(t\right) $ out of the system. $ \mathbf{Y}\left(t\right)=\mathbf{X}\left(t\right)*h\left(t\right)=\int_{-\infty}^{\infty}\mathbf{X}\left(t-\alpha\right)h\left(\alpha\right)d\alpha=\int_{-\infty}^{\infty}\mathbf{X}\left(\alpha\right)h\left(t-\alpha\right)d\alpha. $
Important Facts
1. If the input to a LTI system is a Gaussian random process, the output is a Gaussian random process.
2. If the input to a stable L.T.I. system is S.S.S., so is the output. L.T.I. system is stable if $ \int_{-\infty}^{\infty}\left|h\left(t\right)\right|dt<\infty. $
Fundamental Theorem
• For any linear system we will encounter $ E\left[L\left[\mathbf{X}\left(t\right)\right]\right]=L\left[E\left[\mathbf{X}\left(t\right)\right]\right]. $
• Applying this to a L.T.I. system, we get $ E\left[\mathbf{Y}\left(t\right)\right]=E\left[\int_{-\infty}^{\infty}\mathbf{X}\left(t-\alpha\right)h\left(\alpha\right)d\alpha\right]=\int_{-\infty}^{\infty}E\left[\mathbf{X}\left(t-\alpha\right)h\left(\alpha\right)\right]d\alpha=\int_{-\infty}^{\infty}\eta_{\mathbf{X}}\left(t-\alpha\right)h\left(\alpha\right)d\alpha. $$ \therefore\eta_{\mathbf{Y}}\left(t\right)=E\left[\mathbf{Y}\left(t\right)\right]=\eta_{\mathbf{X}}\left(t\right)*h\left(t\right). $
Output Autocorrelation
$ R_{\mathbf{YY}}\left(t_{1},t_{2}\right)=E\left[\mathbf{Y}\left(t_{1}\right)\mathbf{Y}\left(t_{2}\right)\right]=E\left[\int_{-\infty}^{\infty}\mathbf{X}\left(t_{1}-\alpha\right)h\left(\alpha\right)d\alpha\cdot\int_{-\infty}^{\infty}\mathbf{X}\left(t_{2}-\beta\right)h\left(\beta\right)d\beta\right] $$ =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}E\left[\mathbf{X}\left(t_{1}-\alpha\right)\mathbf{X}\left(t_{2}-\beta\right)\right]h\left(\alpha\right)h\left(\beta\right)d\alpha d\beta $$ =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}R_{\mathbf{XX}}\left(t_{1}-\alpha,t_{2}-\beta\right)h\left(\alpha\right)h\left(\beta\right)d\alpha d\beta. $
Theorem
If the input to a stable LTI system is WSS, so is the output.