2.1 Converge
Definition. Converge
A sequence of numbers x1,x2,⋅⋅⋅,xn,⋅⋅⋅ is said to converge to a limit x if, for every ε > 0 , there exists a number $ n_{\epsilon}\in\mathbf{N} $ such that
$ \left|x_{n}-x\right|<\epsilon,\;\forall n\geq n_{\epsilon} $.
"xn→x as n→∞".
Given a random sequence $ \mathbf{X}_{1}\left(\omega\right),\mathbf{X}_{2}\left(\omega\right),\cdots,\mathbf{X}_{n}\left(\omega\right),\cdots $ for any particular ω0∈S , we have $ \mathbf{X}_{1}\left(\omega_{0}\right),\mathbf{X}_{2}\left(\omega_{0}\right),\cdots,\mathbf{X}_{n}\left(\omega_{0}\right) $ is a sequence of real numbers.
• It may converge to a number $ \mathbf{X}\left(\omega_{0}\right) $ that may be a function of ω0 .
• It may not converge.
Most likely, $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ converge for some ω∈S and will diverge for other ω∈S . When we study stochastic convergence, we study the set A⊂S for which $ \mathbf{X}_{1}\left(\omega\right),\mathbf{X}_{2}\left(\omega\right),\cdots,\mathbf{X}_{n}\left(\omega\right),\cdots $ is a convergent sequence of real numbers.
2.1.1 Definition. Converge everywhere
We say a sequence of random variables converges everywhere (e) if the sequence $ \mathbf{X}_{1}\left(\omega\right),\mathbf{X}_{2}\left(\omega\right),\cdots,\mathbf{X}_{n}\left(\omega\right),\cdots $ each converge to a number $ \mathbf{X}\left(\omega\right) $ for each $ \omega\in\mathcal{S} $ .
Note
• The number $ \mathbf{X}\left(\omega\right) $ that $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ converges to is in general a function of ω .
• Convergence (e) is too strong to be useful.
2.1.2 Definition. Converge almost everywhere
A random sequence $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ converges almost everywhere (a.e.) if the set of outcomes $ A\subset\mathcal{S} $ such that $ \mathbf{X}_{n}\left(\omega\right)\rightarrow\mathbf{X}\left(\omega\right),\;\omega\in A $ exists and has probability 1: $ P\left(A\right)=1 $ . Other names for this are: almost surely (a.s.) and convergence with probability one. We write this as “$ \mathbf{X}_{n}\rightarrow(a.e)\rightarrow\mathbf{X} $ ” or “$ P\left(\left\{ \mathbf{X}_{n}\rightarrow\mathbf{X}\right\} \right)=1. $ ”
2.1.3 Definition. Converge in mean-square
We say that a random sequence converges in mean-square (m.s.) to a random variable $ \mathbf{X} $ if $ E\left[\left|\mathbf{X}_{n}-\mathbf{X}\right|^{2}\right]\rightarrow0\textrm{ as }n\rightarrow\infty $.
Note Convergence (m.s.) is also called “limit in the mean convergence” and is written “l.i.m. $ \mathbf{X}_{n}=\mathbf{X} $ ” (bad). Better notation is $ \mathbf{X}_{n}\rightarrow(m.s.)\rightarrow\mathbf{X} $ .
2.1.4 Definition. Converge in probability
A random sequence $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ converges in probability (p) to a random variable $ \mathbf{X} $ if, $ \forall\epsilon > 0 P\left(\left\{ \left|\mathbf{X}_{n}-\mathbf{X}\right|>\epsilon\right\} \right)\rightarrow0 $ as $ n\rightarrow\infty $. As opposed to $ P\left(\left\{ \mathbf{X}_{n}\rightarrow(a.e.)\rightarrow\mathbf{X}\right\} \right) $ . Convergence (a.e.) is a much stronger form of convergence.
2.1.5 Definition. Converge in distribution
A random sequence $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ converges in distribution (d) to a random variable $ \mathbf{X} $ if $ F_{\mathbf{X}_{n}}\left(x\right)\rightarrow F_{\mathbf{X}}\left(x\right) $ at every point $ x\in\mathbf{R} $ where $ F_{\mathbf{X}}\left(x\right) $ is continuous.
Example: Central Limit Theorem
2.1.6 Definition. Converge in density
A random sequence $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ converges in density (density) to a random variable $ \mathbf{X} if f_{\mathbf{X}_{n}}\left(x\right)\rightarrow f_{\mathbf{X}}\left(x\right)\textrm{ as }n\rightarrow\infty $ for every $ x\in\mathbf{R} $ where $ F_{\mathbf{X}}\left(x\right) $ is continuous.
2.1.7 Convergence in distribution vs. convergence in density
• Aren't convergence in density and distribution equivalent? NO!
• Example: Let $ \left\{ \mathbf{X}_{n}\left(\omega\right)\right\} $ be a sequence of random variables with $ \mathbf{X}_{n} $ having pdf $ f_{\mathbf{X}_{n}}\left(x\right)=\left[1+\cos\left(2\pi nx\right)\right]\cdot\mathbf{1}_{\left[0,1\right]}\left(x\right) $. $ f_{\mathbf{X}_{n}}\left(x\right) $ is a valid pdf for $ n=1,2,3,\cdots $. The cdf of $ \mathbf{X}_{n} $ is $ F_{\mathbf{X}_{n}}\left(x\right)=\left\{ \begin{array}{lll} 0 , x<0\\ x+\frac{1}{2\pi n}\sin\left(x2\pi n\right) , x\in\left[0,1\right]\\ 1 , x>1. \end{array}\right. $
• Now define $ F_{\mathbf{X}}\left(x\right)=\left\{ \begin{array}{lll} 0 , x<0\\ x , x\in\left[0,1\right]\\ 1 , x>;1. \end{array}\right. $
• Because $ F_{\mathbf{X}_{n}}\left(x\right)\rightarrow F_{\mathbf{X}}\left(x\right) $ as $ n\rightarrow\infty ,\therefore\mathbf{X}_{n}\rightarrow\left(d\right)\rightarrow\mathbf{X} $.
• The pdf of $ \mathbf{X} $ corresponding to $ F_{\mathbf{X}}\left(x\right) $ is $ f_{\mathbf{X}}\left(x\right)=\mathbf{1}_{\left[0,1\right]}\left(x\right) $.
• What does $ f_{\mathbf{X}_{n}}\left(x\right) $ look like? We do not have convergence in density.
• $ \therefore $ Convergence in density and convergence in distribution are NOT equivalent. In fact, convergence (density) $ \left(\nLeftarrow\right)\Longrightarrow $ convergence (distribution)
2.1.8 Cauchy criterion for convergence
Recall that a sequence of numbers $ x_{1},x_{2},\cdots,x_{n} $ converges to $ x $ if $ \forall\epsilon>0 , \exists n_{\epsilon}\in\mathbf{N} $ such that $ \left|x_{n}-x\right|<\epsilon,\;\forall n\geq n_{\epsilon} $. To use this definition, you must know $ x $ . The Cauchy criterion gives us a way to test for convergence without knowing the limit $ x $ .
Cauchy criterion
If $ \left\{ x_{n}\right\} $ is a sequence of real numbers and $ \left|x_{n+m}-x_{n}\right|\rightarrow0 $ as $ n\rightarrow\infty $ for all $ m\in\mathbf{N} $ , then $ \left\{ x_{n}\right\} $ converges to a real number.
Note
The Cauchy criterion can be applied to various forms of stochastic convergence. We look at:
$ \mathbf{X}_{n}\rightarrow\mathbf{X} $ (original)
$ \mathbf{X}_{n} and \mathbf{X}_{n+m} $ (Cauchy criterion)
e.g.
If $ \varphi\left(n,m\right)=E\left[\left|\mathbf{X}_{n}-\mathbf{X}_{n+m}\right|^{2}\right]\rightarrow0 $ as $ n\rightarrow\infty $ for all $ m=1,2,\cdots $ , then $ \left\{ \mathbf{X}_{n}\right\} $ converges in mean-square.
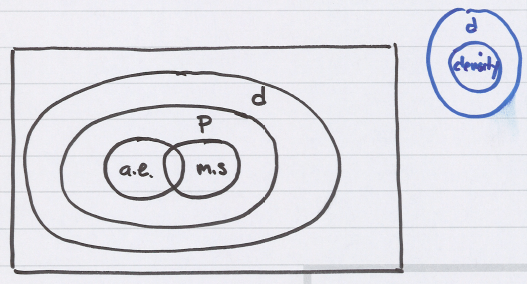
2.1.9 Comparison of modes of convergence
convergence $ \left(m.s.\right) \Longrightarrow $ convergence $ \left(p\right) $
$ p\left(\left\{ \left|\mathbf{X}-\mu\right|>\epsilon\right\} \right)\leq\frac{E\left[\left(\mathbf{X}-\mu\right)^{2}\right]}{\epsilon^{2}}=\frac{\sigma_{\mathbf{X}}^{2}}{\epsilon^{2}} $
$ \Longrightarrow p\left(\left\{ \left|\mathbf{X}_{n}-\mathbf{X}\right|>\epsilon\right\} \right)\leq\frac{E\left[\left(\mathbf{X}_{n}-\mathbf{X}\right)^{2}\right]}{\epsilon^{2}}. $
Thus, $ m.s. $ convergence $ \Longrightarrow E\left[\left(\mathbf{X}_{n}-\mathbf{X}\right)^{2}\right]\rightarrow0 $ as $ n\rightarrow\infty \Longrightarrow p\left(\left\{ \left|\mathbf{X}_{n}-\mathbf{X}\right|>\epsilon\right\} \right)\rightarrow0 $ as $ n\rightarrow\infty $ .
convergence $ \left(a.e.\right) \Longrightarrow $ convergence $ \left(p\right) $
Follows from definitions, converse is not true.
convergence $ \left(d\right) $ is “weaker than” convergence $ \left(a.e.\right) $ , $ \left(m.s.\right) $ , or $ \left(p\right) $ .
$ \left(a.e.\right)\Rightarrow\left(d\right) , \left(m.s.\right)\Rightarrow\left(d\right) $ , and $ \left(p\right)\Rightarrow\left(d\right) $ .
Note
$ \left(a.e.\right)\nRightarrow\left(m.s.\right) $ and $ \left(m.s.\right)\nRightarrow\left(a.e.\right) $ .
Note
The Chebyshev inequality is a valuable tool for working with $ m.s. $ convergence.