Communication, Networking, Signal and Image Processing (CS)
Question 5: Image Processing
August 2016 (Published in Jul 2019)
Problem 1
1. Calcualte an expression for $ \lambda_n^c $, the X-ray energy corrected for the dark current
$ \lambda_n^c=\lambda_n^b-\lambda_n^d $
2. Calculate an expression for $ G_n $, the X-ray attenuation due to the object's presence
$ G_n = \frac{d\lambda_n^c}{dx}=-\mu (x,y_0+n * \Delta d)\lambda_n^c $
3. Calculate an expression for $ \hat{P}_n $, an estimate of the integral intensity in terms of $ \lambda_n $, $ \lambda_n^b $, and $ \lambda_n^d $
$ \lambda_n = (\lambda_n^b-\lambda_n^d) e^{-\int_{0}^{x}\mu(t)dt}d)\lambda_n^c $
$ \hat{P}_n = \int_{0}^{x}\mu(t)dt= -log(\frac{\lambda_n}{\lambda_n^b-\lambda_n^d}) $
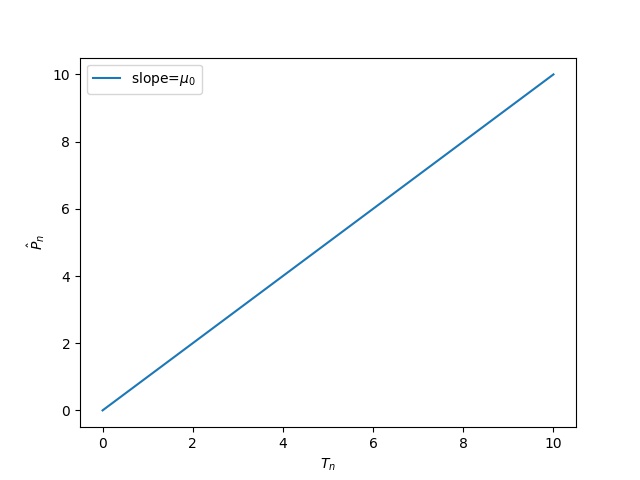
4. For this part, assume that the object is of constant density with $ \mu(x,y) = \mu_0 $. Then sketch a plot of $ \hat{P}_n $ versus the object thickness, $ T_n $, in mm, for the $ n^{th} $ detector. Label key features of the curve such as its slope and intersection.
Problem 2
1. Specify the size of $ YY^t $ and $ Y^tY $. Which matrix is smaller
Y is of size $ p \times N $, so the size of $ YY^t $ is $ p \times p $
Y is of size $ p \times N $, so the size of $ Y^tY $ is $ N \times N $
Obviously, the size of $ Y^tY $ is much smaller, since N << p.
2. Prove that both $ YY^t $ and $ Y^tY $ are both symmetric and positive semi-definite matrices.
To prove it is symmetric:
$ (YY^t)^t = YY^t $
To prove it is positive semi-definite:
Let x be an arbitrary vector
$ x^tYY^tx = (Y^tx)^T(Y^tx) \geq 0 $ so the matrix of $ YY^t $ is positive semi-definite.
The proving procedures for $ Y^tY $ are the same
3. Derive expressions for $ V $ and $ \Sigma $ in terms of $ T $, and $ D $.
$ Y^tY = (U \Sigma V^t)^T U \Sigma V^t = V\Sigma^2 V^t = TDT^t $ therefore $ V =T $ and $ \Sigma = D^{\frac{1}{2}} $
4. Derive an expression for $ U $ in terms of $ Y $, $ T $, $ D $.
$ Y = U\Sigma V^t= UD^{\frac{1}{2}}T^t $
$ \therefore U = Y(D^{\frac{1}{2}}T^t)^{-1} $
5. Derive expressions for E in terms of Y, T, and D.
$ YY^t = U\Sigma V^t(U\Sigma V^t)^t= U\Sigma^2 U^t = E\Gamma E^t $
therefore
$ E = U = Y(D^{\frac{1}{2}}T^t)^{-1} $
6. If the columns of Y are images from a training database, then what name do we give to the columns of U?
They are called eigenimages.