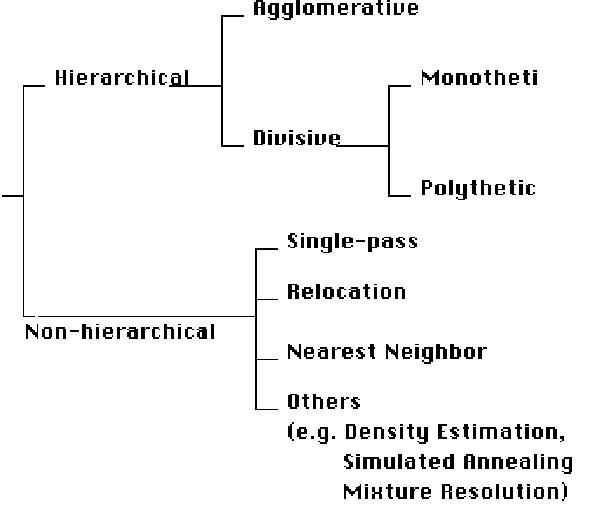
Types of Clustering Methods
- Partitioning Methods:
The partitioning method divides a data set into M different clusters, where each object belongs to one of these clusters. Each cluster has a representative element, or centroid, which describes all the objects contained in that cluster. In some cases, the arithmetic mean of the attribute vectors of all the objects in the cluster is a good representative.
Method: This method determines the clusters of a data set in one pass, and runs in O(NlogN). The disadvantage of this method is that it is highly dependent on the order in which the objects are processed.
I. Set the 1st object as the centroid for the 1st cluster.
II. Calculate S (similarity coefficient) for each object with each existing centroid.
III. If the calculated S for a specific object is higher than a given threshold, add the object to the corresponding cluster, and recalculate the centroid for this cluster. If the S value is lower than the threshold, create a new cluster. If at the end some objects have not been clustered, repeat Step II.
- Hierarchical Agglomerative Methods:
Method: This method determines clusters by adding the closest pair of objects to a single cluster. This algorithm run in N^3 time.
I. Determine which 2 objects are closest to each other, and insert them into one cluster.
II. Determine the next 2 closest objects. (Note: In this step, an object can be a single object or a cluster)
III. If at the end, some objects have not been clustered, repeat Step II.
Various Clustering Algorithms
Description: This is a link to the Speech and Image Processing group at Joensuu Science Park in Finland. It includes links to many programs and pseudo codes which are intended for clustering data sets with an undetermined number of clusters. These programs address the two problems commonly faced in clustering applications: determining the number of clusters in the data set, and finding the location of each of these clusters. Since clustering is considered an NP-complete problem, ideal solutions have exponential running time. For this reason, the algorithms presented by this group are sub-optimal, but run in polynomial time. [1]
k-centers clustering: The k-centers clustering algorithms is a partitioning clustering algorithm in the classical sense. By Mimi's categorization, it requires the knowledge of the full feature vectors. The algorithm tries to partition the data into 'k' clusters such that maximum diameter of the clusters is minimized. The diameter of a cluster is given by the maximum distance between a pair of points in a cluster. Its roots can be traced by to the facility location problem. The problem is, given a graph, we have to find 'k' special nodes such that maximum distance of a node (other than the special nodes) to its closest special node is minimized. The nice thing about this clustering problem is that there exists efficient approximation algorithms (up to a factor of 2) for this problem. The requirement for them is that the distance between the points should be a metric. For more see, [2], [www.cs.umd.edu/~samir/858/lec16.ps]

