Audio Signal Filtering

Background

Audio signals in the digital world are simply 1-D signals that contain the values of the sampled sound v/s an index, say k.
Consider the diaphragm on a microphone, that vibrates every time a sound impinges on it.
The vibration is converted to an electrical signal by a transducer, which then relays the "analog" signal to an A/D converter.
Finally, the A/D converter samples the analog signal, and makes it a train of samples; each box of the train contains a value.
This value corresponds to the digital representation of the electrical signal that resulted from the vibration.
For example, say the diaphragm vibrated 0.2mm, resulting in a generated voltage of 0.2mV (these values are completely arbitrary).
If the A/D converter designated 0V to x00 and 10mV to xFF, then the resolution of designating values to the samples would be 10/255 mV or .04mV. Thus, 0.2 mV would be x05.
This value would be stored in the digital sound file, against a time index corresponding to when the A/D received this sample.
Since this page focuses on Audio Signal filtering, those interested in the basics of Audio Processing can go to the references on the following wiki:
http://en.wikipedia.org/wiki/Digital_audio

This page took a long time to figure out. Mainly because, for images and sine waves, it's easy to find some that aren't copyrighted.
For images you just use your pet dog's best photograph, and for sine waves, you write a line in MATLAB.
But for audio signals, almost every recorded sound is copyrighted in some way or the other, and to avoid being sued for copyright infringement, I had to find sounds to play with, and publish online, that weren't "owned", so to speak.
Fortunately, however, animals don't take you to court for stealing their sounds, so that's just what I did.
On this page, I experiment with two animal sounds; the first is a high-frequency bird pitch, while the second is a low-frequency bear rumble.
Another issue which makes audio different from images is the fact that the index n in the x[n] of signals represents the space variable, whereas in audio this is time.

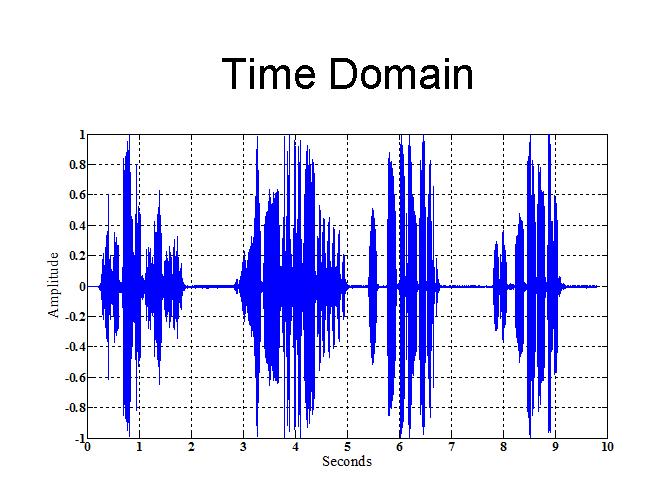
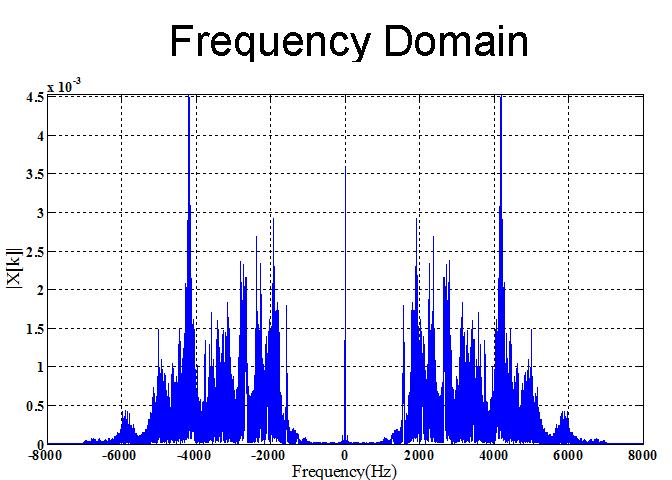
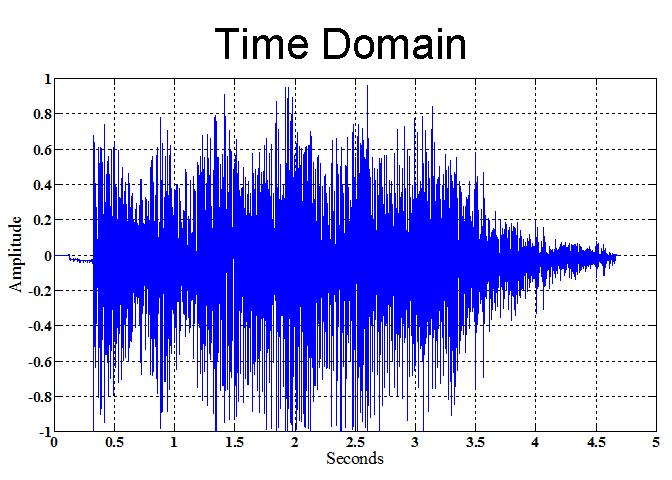
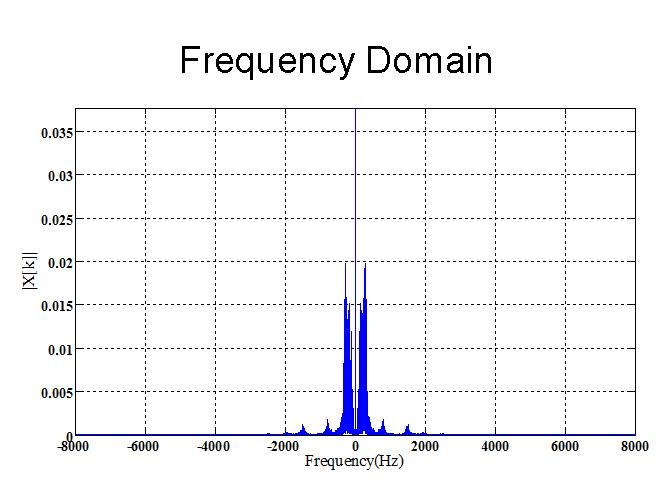
In the following figure, you can see what the sound looks like both in the time domain, and the frequency domain.

The code for the above can be obtained here: Code:Song_bird:part1
As expected, most of the energy of the signal, in this case the bird's high frequency voice, is concentrated in the frequency band of around 2000 - 6000 Hz.
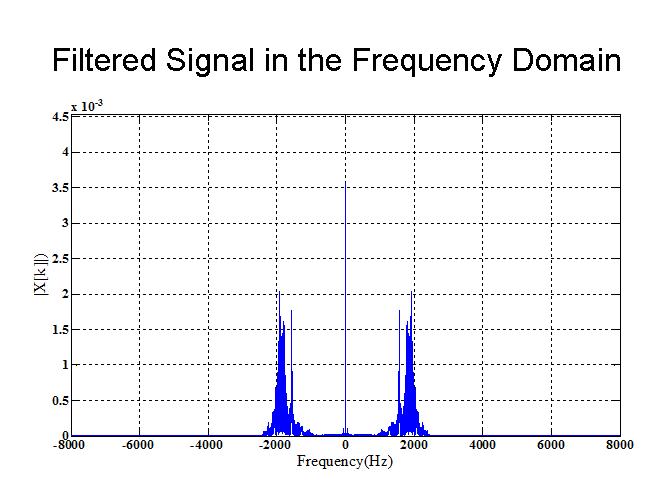
To filter this out, we can apply a low-pass filter with a cutoff frequency of around 2000 Hz.

Looks like we killed most of the bird's energy, and it's kind of obvious that we would hear a very low frequency low energy chirp now. See (hear) for yourself.

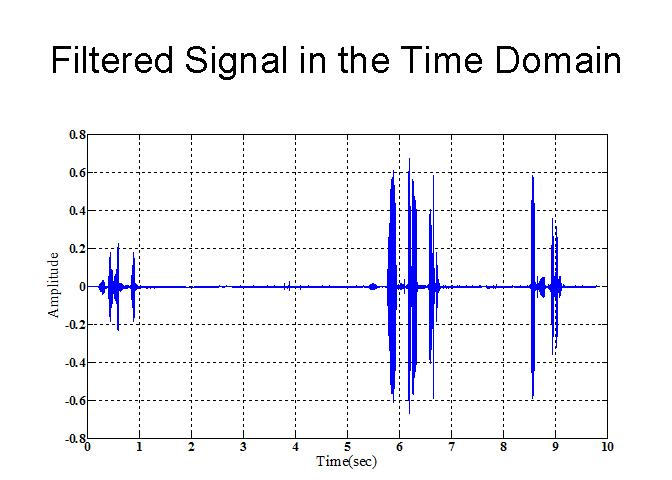
Also, since we've killed so much of the signal, it should also be obvious that the signal looks much more different in the time domain as well. Here's how.

Now, consider a low-pitch bear rumble that sounds something like this
- Media:bear.wav
The signal in the time and frequency domains looks as shown below

Again, as expected, the guttural groan of the bear lies mostly in the low frequency region, coincidentally, below the 2000 Hz region (It's almost like the bird and the bear recorded for this page :)).
So adding a high pass filter should remove the bear's voice completely.
Since you've already seen how the signals look in the time and frequency domain post filtering, I won't present the figures again, for sake of space.
I do present the code and the audio though, so you can try it yourself.
- Media:bear_filtered.wav
- Code:bear
It is interesting to note that we can now hear crickets in the background after removing the bear from the picture. The bear's groan was so loud, that it masked the low amplitude, high frequency insects in the background.

Here I have presented a very basic treatment of two sounds of nature, each sound containing a unique band of frequencies.
This technique, in a rough sense, can be applied to isolate different animals from a wildlife researcher's recording of a noisy forest.
Eg: if we had this kind of recording, Media:forest.wav, all we need to study just the bird is to high pass filter the signal, and conversely, low pass filter to hear the bear.