I'm not too sure but I think that the PDF of L can be directly related to the PDF of r. I say this because for any given point D on the range [0,r] there are going to be infinitely many chords of length L.
The following picture has an external circle of radius r, and an internal circle of radius D. Any chord at distance D from the center must be tangent to this internal circle (because otherwise it would be a chord at a different distance from the center).
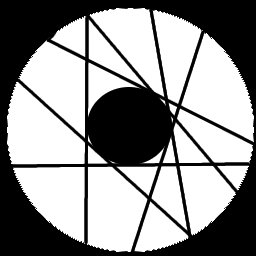
I think this means that if you find the range of lengths L (which is clearly just [0,2r], that the PDF of it should be a uniform distribution, as each distance has an infinite amount of chords tangent to a circle of radius D. My only concerns is that at the point 0. I don't know how to describe it well, but with a D > 0, each point on a circle has 2 lines tangent to the circle (which can be seen in the above picture). But when D = 0, each point has exactly 1 line that goes through the center. This doesnt change the fact however that even when D = 0, there are an infinite amount of chords that go through that point.
Can anyone back up my suspicion that L should be have uniform PDF?
--- Beau's Comments
Hey AJ, I agree with most of your explaination, but I am not sure about L having uniform PDF...
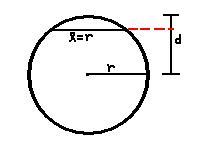
From my poorly drawn image, I show the circle with radius r. d is the possible distances the chord my have from r. The picture shows that there is a smaller possiblity for l to be less than or equal to the length of r. I am thinking the distribution is exponential...